Question

A sculptor is planning to make two triangular prisms out of steel. The sculptor will use for the bases of one prism and for the bases of the other prism. (a)Is triangle 1 similar to triangle 2?(b)Suppose the sculptor makes both prisms with the same height. Which prism will have a greater volume? How many times greater? Show your work.

Answer 1

To figure out if both triangles are similar, we will use the relation below

`\begin{gathered} (AB)/(DE)=(BC)/(EF) \\ (40)/(48)=(30)/(36) \\ (5)/(6)=(5)/(6) \end{gathered}`

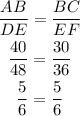
The two triangles both have the same scale factors as

`=(5)/(6)`

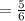
The ratio of their corresponding sides are equal therefore,

Triangle 1 is similar to triangle 2,and the included angles are equal because they are both 90°, so by the SAS similarity theorem, the two triangles are similar.

b) Suppose the sculptor makes both prisms with the same height.

To determine the prism to have the great volume, we will first calculate the volume factor

`\text{volume factor=(sacle factor)}^3`

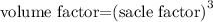
By substituting the values, we will have

`\begin{gathered} \text{volume factor=(sacle factor)}^3 \\ \text{volume factor=}=((5)/(6))^3 \\ \text{volume factor=}(125)/(216) \end{gathered}`

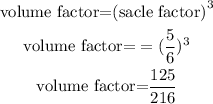
Let the volume of the from triangle 1 be

Let the volume from triangle 2 be

Volume of the smaller prism will be

`\begin{gathered} V_{\text{small}}=(1)/(2)*40*30* h \\ V_{\text{small}}=600h \end{gathered}`

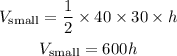
Volume of the larger prism will be

`\begin{gathered} V_{\text{big}}=(1)/(2)*48*36* h \\ V_{\text{big}}==864h \end{gathered}`

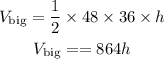
Hence,'

To determine the number of times the larger prism is bigger than the smaller prism, we will use the formula below

`\begin{gathered} =(864h)/(600h) \\ =1.44 \end{gathered}`

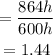
Hence,

The volume of the prism from triangle 2 is 1.44 times greater than the volume from triangle 1