Answer:
To figure out if both triangles are similar, we will use the relation below
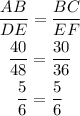
The two triangles both have the same scale factors as
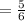
The ratio of their corresponding sides are equal therefore,
Triangle 1 is similar to triangle 2,and the included angles are equal because they are both 90°, so by the SAS similarity theorem, the two triangles are similar.
b) Suppose the sculptor makes both prisms with the same height.
To determine the prism to have the great volume, we will first calculate the volume factor
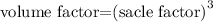
By substituting the values, we will have
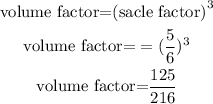
Let the volume of the from triangle 1 be
Let the volume from triangle 2 be
Volume of the smaller prism will be
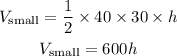
Volume of the larger prism will be
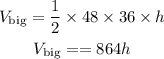
Hence,'
To determine the number of times the larger prism is bigger than the smaller prism, we will use the formula below
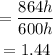
Hence,
The volume of the prism from triangle 2 is 1.44 times greater than the volume from triangle 1