Question

APPLICATIONS5. SAT scores are normally distributed with a mean of 500 points and standard deviation of 100 points.If Jenna earns 700 points, she did better than what percent of students who took the SAT?

Answer 1

97.73%

Explanation:

SAT scores are normally distributed with:

• Mean = 500

,

• Standard deviation = 100

We want to find out what percentage of the students who took SAT scored less than Jenna if Jenna earns 700 points.

In order to do this, we first find the z-score using the formula below:

`z-score=(X-\mu)/(\sigma)\text{ where }\begin{cases}{X=Raw\;Score} \\ {\mu=mean} \\ {\sigma=Standard\;Deviation}\end{cases}`

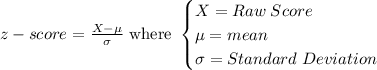
For a raw score, X = 700:

Therefore, Jenna did better than 97.73% of students who took the SAT.