Graphing a Quadratic Equation
Let's take as an example the function:
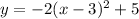
The vertex form of a quadratic function is:
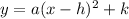
Where a is the leading coefficient and (h,k) is the vertex.
If a is positive, the function is concave up, if negative the function is concave down.
The first step is to obtain the parameters by comparing the given equation with the general equation.
Thus, we have: a = -2. Vertex = (3,5)
Now we locate the vertex in the coordinate plane and draw the parabola opening down.
For more precision, we can substitute some points around the vertex, like for example:
x={1,2,4,5}
We get the y-coordinates:
y={-3,3,3,-3}
Then we plot the graph as follows: