The value of a machine at the end of t years with a rate of depreciation, r is given by the function:
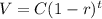
It is required to find the age of a machine that originally costs $13,500, but is now valued at $10,419 and has a rate of depreciation of 0.12.
To do this, substitute C=13500, V=10419, and r=0.12 into the function:
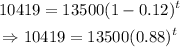
Solve the resulting equation for t:

Take the Logarithm of both sides:
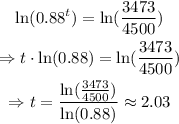
Hence, the machine is about 2.03 years.
The machine is about 2.03 years.