Question

A 14-foot ladder is leaning against a house with the base of the ladder 6 feet from the house. How high up the house does the ladder reach? If necessary, round to the nearest tenth foot.

Answer 1

`12.6\text{ ft (option }B)`

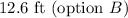
Step-by-step explanation:

The ladder leaning on the house formed a right angled triangle

Using an illustration from the diagram given:

To get the height the house makes with the ladder, we will apply pythagoras' theorem:

Hypotenuse² = opposite² + adjacent²

`\begin{gathered} \text{hypotenuse = 14, adjacent = 6, opposite = }? \\ 14^2=opposite^2+6^2 \\ 196\text{ = }opposite^2\text{ + 36} \\ \\ \text{subtract 36 from both sides:} \\ 196\text{ - 36 = }opposite^2 \\ 160\text{ = }opposite^2 \end{gathered}`