ANSWER
• Distance:, 7.81
,
• Midpoint: ,(-4.5, -6)
Step-by-step explanation
The distance between two points (x₁, y₁) and (x₂, y₂) is given by the Pythagorean Theorem,
![d=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2_{}}](https://img.qammunity.org/2023/formulas/mathematics/college/45856wqkd7p0q5e9z533lj5djbmuqd7gt9.png)
In this problem, the points are (-7, -9) and (-2, -3),
![\begin{gathered} d=\sqrt[]{(-7-(-2))^2+(-9-(-3))^2} \\ d=\sqrt[]{(-7+2)^2+(-9+3)^2}\text{ } \\ d=\sqrt[]{(-5)^2+(-6)^2}=\sqrt[]{25+36} \\ d=\sqrt[]{61}\approx7.81 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1nojjoismyy1r6w3y8lf35qd54s38v1onp.png)
Hence, the distance between P1 and P2 is 7.81 units.
To find the midpoint, we have to find the average between the coordinates of the points,
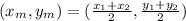
The midpoint in this problem is,
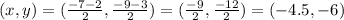
Hence, the midpoint between P1 and P2 is (-4.5, -6).