Question

Could you please help me with this exercise? Thanks for your help!

Answer 1

• Distance:, 7.81

,

• Midpoint: ,(-4.5, -6)

Step-by-step explanation

The distance between two points (x₁, y₁) and (x₂, y₂) is given by the Pythagorean Theorem,

`d=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2_{}}`

In this problem, the points are (-7, -9) and (-2, -3),

`\begin{gathered} d=\sqrt[]{(-7-(-2))^2+(-9-(-3))^2} \\ d=\sqrt[]{(-7+2)^2+(-9+3)^2}\text{ } \\ d=\sqrt[]{(-5)^2+(-6)^2}=\sqrt[]{25+36} \\ d=\sqrt[]{61}\approx7.81 \end{gathered}`

Hence, the distance between P1 and P2 is 7.81 units.

To find the midpoint, we have to find the average between the coordinates of the points,

`(x_m,y_m)=\mleft((x_1+x_2)/(2),(y_1+y_2)/(2)\mright)`

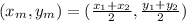
The midpoint in this problem is,

`(x,y)=\mleft((-7-2)/(2),(-9-3)/(2)\mright)=\mleft((-9)/(2),(-12)/(2)\mright)=(-4.5,-6)`

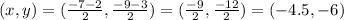
Hence, the midpoint between P1 and P2 is (-4.5, -6).