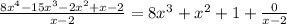We want to calculate the following division
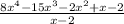
Using the long division method, we start by dividing the leading term of the dividend by the leading term of the divisor
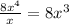
Then, we multiply it by the divisor
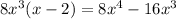
then, subtract the dividend from the obtained result

Then, our division can be rewritten as
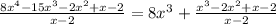
Repeating the whole process for the remaining division, we have
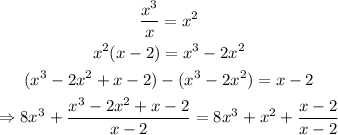
Repeating the whole process again, we have our result