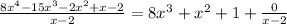Question

Rewrite (8x4 – 15x3 – 2x2 + x – 2)/(x – 2) using long division method in the form q(x) + r(x)/b(x) where q(x) = quotient, r(x) = remainder, and b(x) = divisor.

Answer 1

We want to calculate the following division

`(8x^4-15x^3-2x^2+x-2)/(x-2)`

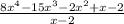
Using the long division method, we start by dividing the leading term of the dividend by the leading term of the divisor

`(8x^4)/(x)=8x^3`

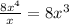
Then, we multiply it by the divisor

`8x^3(x-2)=8x^4-16x^3`

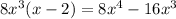
then, subtract the dividend from the obtained result

`(8x^4-15x^3-2x^2+x-2)-(8x^4-16x^3)=x^3-2x^2+x-2`

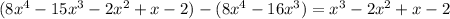
Then, our division can be rewritten as

`(8x^4-15x^3-2x^2+x-2)/(x-2)=8x^{3^{}}+(x^3-2x^2+x-2)/(x-2)`

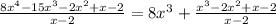
Repeating the whole process for the remaining division, we have

`\begin{gathered} (x^3)/(x)=x^2 \\ x^2(x-2)=x^3-2x^2 \\ (x^3-2x^2+x-2)-(x^3-2x^2)=x-2 \\ \Rightarrow8x^{3^{}}+(x^3-2x^2+x-2)/(x-2)=8x^{3^{}}+x^2+(x-2)/(x-2) \end{gathered}`

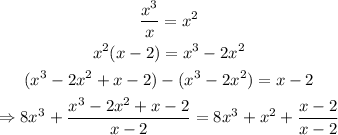
Repeating the whole process again, we have our result

`(8x^4-15x^3-2x^2+x-2)/(x-2)=8x^{3^{}}+x^2+1+(0)/(x-2)`