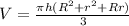Question

How to calculate volume of a bucket that's cut from a cone?

Answer 1

Given: A frustum of a cone.

Required: To determine the formula for the frustum of a cone.

Step-by-step explanation: When a cone is divided into two parts, the upper part remains in the shape of a cone, and the lower part makes the frustum.

The formula gives the volume of a cone-

`V=(1)/(3)\pi r^2h`

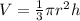
The general formula gives the volume of the frustum as-

`V=(h)/(3)(S_1+S_2+√(S_1S_2)`

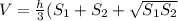
where h denotes the height, S1 and S2 are the base surface areas. Here we have-

`\begin{gathered} S_1=\pi R^2 \\ S_2=\pi r^2 \end{gathered}`

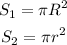
Here, R and r are the radius of the base at the bottom and top of the frustum, respectively.

Substituting the values into the formula for frustum as-

`V=(h)/(3)(\pi R^2+\pi r^2+√((\pi R^2)(\pi r^2))`

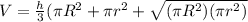
Further solving-

`V=(\pi h)/(3)(R^2+r^2+Rr)`

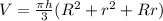
Final Answer: The volume of the frustum is-

`V=(\pi h(R^2+r^2+Rr))/(3)`