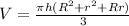Given: A frustum of a cone.
Required: To determine the formula for the frustum of a cone.
Step-by-step explanation: When a cone is divided into two parts, the upper part remains in the shape of a cone, and the lower part makes the frustum.
The formula gives the volume of a cone-
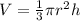
The general formula gives the volume of the frustum as-
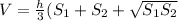
where h denotes the height, S1 and S2 are the base surface areas. Here we have-
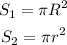
Here, R and r are the radius of the base at the bottom and top of the frustum, respectively.
Substituting the values into the formula for frustum as-
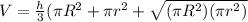
Further solving-
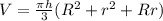
Final Answer: The volume of the frustum is-