Question

What is the behavior of the graph y = 22³ +2²-7a-6 at each of its zeros?OA. two resemble a linear function and one resembles a quadratic functionB. they all resemble a linear functionOC. they all resemble a cubic functionD. cannot be determinedReset Selection

Answer 1

B. they all resemble a linear function

Step-by-step explanation

We have to find the zeros of this function. Since it is a 3rd-degree polynomial it is expected that there will be 3 zeros, but one or the three of them can have a multiplicity higher than 2, in which case we will find one or two zeros only.

In this case, the zeros of the function are x = -1.5, x = -1, and x = 2, as we can see in the graph,

So we can write the function as,

`y=2(x+1.5)(x+1)(x-2)`

If we replace each zero in the function, but only for the factors not corresponding to that zero, we will get only one factor. For example, replacing x = 2,

`y=2(2+1.5)(2+1)(x-2)=2\cdot3.5\cdot3(x-2)=21(x-2)`

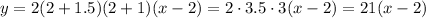
Which is a linear function. And this happens also for both remaining zeros.

Hence, all three zeros resemble a linear function.