we write two equations to solve the numbers
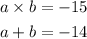
solve a from the second equation
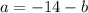
and replace on the first
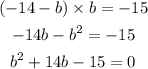
factor by any method to find b
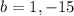
now replace b on any equation to find a

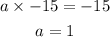
the values of and b must be -15 and 1
Second
write the equations
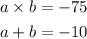
solve a from the second equation

replace on first
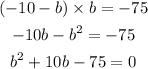
factor to solve
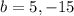
we have two solutions, replace each solutions on any equations to know the true
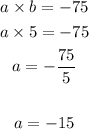

the values of a and b are 5 and -15
Third

solve a from the second equation
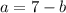
and replace on first
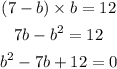
and factor
as we can see the two values that come out of factoring will be the values a and b

so the values of a and b must be 3 and 4