Question

Each diagram below write the 2 numbers on the sides of x that are multiplied together to get the top number of the x, but added together to get the bottom number of the x.

Answer 1

we write two equations to solve the numbers

`\begin{gathered} a* b=-15 \\ a+b=-14 \end{gathered}`

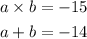
solve a from the second equation

`a=-14-b`

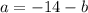
and replace on the first

`\begin{gathered} (-14-b)* b=-15 \\ -14b-b^2=-15 \\ b^2+14b-15=0^{} \end{gathered}`

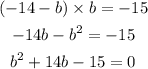
factor by any method to find b

`b=1,-15`

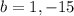
now replace b on any equation to find a

`\begin{gathered} a* b=-15 \\ a*1=-15 \\ a=-15 \end{gathered}`
`\begin{gathered} a*-15=-15 \\ a=1 \end{gathered}`

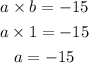
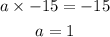
the values of and b must be -15 and 1

Second

write the equations

`\begin{gathered} a* b=-75 \\ a+b=-10 \end{gathered}`

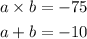
solve a from the second equation

`a=-10-b`

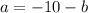
replace on first

`\begin{gathered} (-10-b)* b=-75 \\ -10b-b^2=-75 \\ b^2+10b-75=0 \end{gathered}`

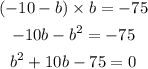
factor to solve

`b=5,-15`

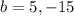
we have two solutions, replace each solutions on any equations to know the true

`\begin{gathered} a* b=-75 \\ a*5=-75 \\ a=-(75)/(5) \\ \\ a=-15 \end{gathered}`
`\begin{gathered} a* b=-75 \\ a*-15=-75 \\ a=(-75)/(-15) \\ \\ a=5 \end{gathered}`

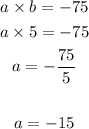
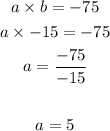
the values of a and b are 5 and -15

Third

`\begin{gathered} a* b=12 \\ a+b=7 \end{gathered}`

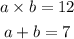
solve a from the second equation

`a=7-b`

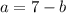
and replace on first

`\begin{gathered} (7-b)* b=12 \\ 7b-b^2=12 \\ b^2-7b+12=0 \end{gathered}`

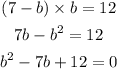
and factor

as we can see the two values ​​that come out of factoring will be the values ​​a and b

`b=3,4`

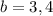
so the values of a and b must be 3 and 4