Question

Two 2 cm-diameter disks spaced 1.396 mm apart form a parallel-plate capacitor. The electric field between the disks is 549,707.592 V/m. An electron is launched from the negative plate. It strikes the positive plate at a speed of 19,424,119.514 m/s. What was the electron's speed as it left the negative plate?

Answer 1

Given:

• Distance between plates = 1.396 mm

,

• Diameter = 2 cm

,

• Electric field = 549,707.592 V/m

,

• Speed = 19,424,119.514 m/s

Let's find the electron's speed as it left the negative plate.

Apply the formula:

`v_i=\sqrt{v_f^2-(2qV)/(m)}`

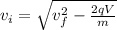
Where:

vf is the final speed = 19,424,119.514 m/s

q = 1.60 x 10⁻¹⁹

V = E x d = 549,707.592 V/m x 1.396 mm

m is the mass of electron = 9.11 x 10⁻³¹ kg

Thus, we have:

`v_i=\sqrt{(19424119.514)^2-(2(1.6*10^(-19))(549707.592)(1.396*10^(-3)))/(9.11*10^(-31))}`

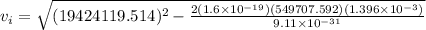
Solving further, we have:

`\begin{gathered} v_i=\sqrt{1.07740573×10^(14)} \\ \\ v_i=10379815.66\text{ m/s} \end{gathered}`

Therefore, the speed as it left the negative plate is 10379815.66 m/s.

ANSWER:

10,379,815.66 m/s