a)
The ratio test states that
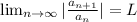
If
• L > 1, the series diverges
• L < 1, the series converges absolutely
• L = 1, inconclusive.
Then let's apply the radio test:
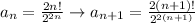
Then
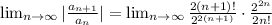
Now we must simplify the expression

Then, we have

The value of r from the ratio test is
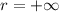
b)
If r > 1, then we can say that the series diverges.