Question

Determine if each set of numbers can be the lengths of the sides of a right triangle.Select the correct text in the table.

Answer 1

Yes

No

Yes

No

Yes

Answer 2

We have to determine the set of numbers is a Pythagorean triple.

It is known that if the square of the largest number is equal to the sum of the squares of the other two numbers, then the number is considered as Pythagorean triple.

The first set of numbers is 5, 12, 13.

Here,

`\begin{gathered} 13^2=12^2+5^2 \\ 169=144+25 \\ 169=169 \end{gathered}`

Thus, the first set is a Pythagorean triple.

The second set of numbers is 12, 35, 20 sqrt 3.

Here,

`\begin{gathered} 35^2=12^2+(20\sqrt[]{3})^2 \\ 1225=144+1200 \\ 1225\\e1344 \end{gathered}`

Thus, the second set is not a Pythagorean triple.

The third set of numbers is 5, 10, 5 sqrt 5.

Here,

`\begin{gathered} (5\sqrt[]{5})^2=10^2+5^2 \\ 125=100+25 \\ 125=125 \end{gathered}`

Thus, the third set of numbers is a Pythagorean triple.

The fourth set of numbers is 8, 12, 15.

Here,

`\begin{gathered} 15^2=12^2+8^2 \\ 225=144+64 \\ 225\\e208 \end{gathered}`

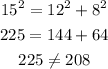
Thus, the fourth set of numbers is not a Pythagorean triple.

The fifth set of numbers is 20, 99, 101.

Here,

`\begin{gathered} 101^2=99^2+20^2 \\ 10201=9801+400 \\ 10201=10201 \end{gathered}`

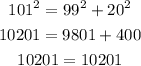
Thus, the fifth set of numbers is a Pythagorean triple.