ANSWER
The pH value is 4.88
Step-by-step explanation
Given information
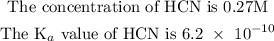
To find the pH of the concentration of the solution, follow the steps below
Step 1: Write the ionic equation of the reaction.
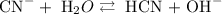
Step 2: write the chemical equilibrium of the reaction
![\begin{gathered} \text{ CN}^-+\text{ H}_2O\text{ }\rightleftarrows\text{ HCN + OH}^- \\ \text{ Initial conc. 0.27 } \\ \text{ Change in conc. - x +x} \\ \text{ Equilibrium \lparen0.27 - x\rparen x} \\ \\ \text{ K}_a\text{ = }\frac{[HCN]}{[CN^-]\frac{}{}\text{ / \lbrack CN}^-]} \end{gathered}](https://img.qammunity.org/2023/formulas/chemistry/college/qh864ci4imm1clfsepuaehkyl7zocy7dxk.png)

Step 3: Find the pH of the solution using the below formula
![\begin{gathered} \text{ pH = -log \lbrack H}^+\text{\rbrack} \\ \text{ pH = -log \lbrack1.294}*10^(-5)] \\ pH\text{ = 4.88} \end{gathered}](https://img.qammunity.org/2023/formulas/chemistry/college/eqhl5h9qlt58u923o23tjjn7f3uzph2cny.png)
Hence, the pH of the solution is 4.88