Question

For a certain company, the cost function for producing x items is C(x) = 40x + 250 and therevenue function for selling x items is R(x) = -0.5(x-80)^2 +3,200. The maximum capacity ofthe company is 120 items.The profit function P(x) is the revenue function R(x) (how much it takes in) minus the cost functionC(x) (how much it spends). In economic models, one typically assumes that a company wants tomaximize its profit, or at least make a profit!Answers to some of the questions are given below so that you can check your work.1. Assuming that the company sells all that it produces, what is the profit function?P(x)=________Hint: Profit=Revenue - Cost as we examined in Discussion 32. What is the domain of P(x)?Hint: Does calculating P (x) make sense when x= -10 or x = 1,000?3. The company can choose to produce either 40 or 50 items. What is their profit for each case, andwhich level of production should they choose?Profit when producing 40 items = ____Profit when producing 50 items = ____4. Can you explain, from our model, why the company makes less profit when producing 10 moreunits?

Answer 1

From the problem, we have the following functions :

Cost Function :

`C(x)=40x+250`

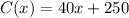
Revenue Function :

`R(x)=-0.5(x-80)^2+3200`

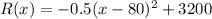
1. Profit function is the difference between the revenue and cost function. This will be :

`\begin{gathered} P(x)=R(x)-C(x) \\ P(x)=\lbrack-0.5(x-80)^2+3200\rbrack-(40x+250) \\ P(x)=\lbrack-0.5(x^2-160x+6400)+3200\rbrack-(40x+250) \\ P(x)=(-0.5x^2+80x-3200+3200)-(40x+250) \\ P(x)=-0.5x^2+80x-40x-250 \\ P(x)=-0.5x^2+40x-250 \end{gathered}`

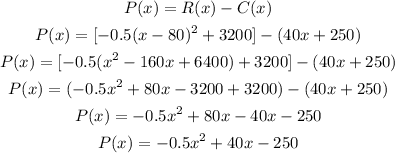
The profit function is :

`P(x)=-0.5x^2+40x-250`

2. The problem states that the maximum capacity of the company is 120 items.

So the domain is all integers from x = 0 to x = 120

3. The profit for x = 40 or 50 are :

`\begin{gathered} \text{when x = 40} \\ P(40)=-0.5(40)^2+40(40)-250 \\ P(40)=550 \\ \text{when x = 50} \\ P(50)=-0.5(50)^2+40(50)-250 \\ P(50)=500 \end{gathered}`

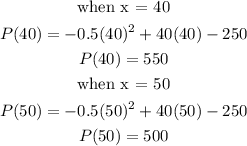
Profit when producing 40 items = 550

Profit when producing 50 items = 500

4. The factor here is the leading term which is -0.5x^2.

Take note that the sign is negative so this term will be deducted from the whole function.

The greater the value it has, the greater the deduction and will give a lesser profit.

Between 40 and 50, 50 will yield a greater deduction value. So producing 10 more units from 40 will make less profit.