From the problem, we have the following functions :
Cost Function :
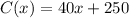
Revenue Function :
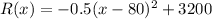
1. Profit function is the difference between the revenue and cost function. This will be :
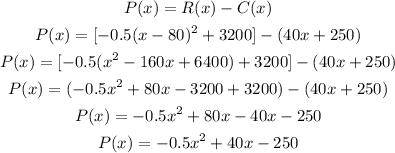
The profit function is :
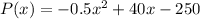
2. The problem states that the maximum capacity of the company is 120 items.
So the domain is all integers from x = 0 to x = 120
3. The profit for x = 40 or 50 are :
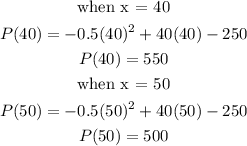
Profit when producing 40 items = 550
Profit when producing 50 items = 500
4. The factor here is the leading term which is -0.5x^2.
Take note that the sign is negative so this term will be deducted from the whole function.
The greater the value it has, the greater the deduction and will give a lesser profit.
Between 40 and 50, 50 will yield a greater deduction value. So producing 10 more units from 40 will make less profit.