The function is
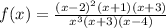
Notice that if we try to evaluate the function at x=0, we would get,
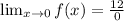
This means that the function f(x) goes to infinity as x approaches zero.
Consider a very small value ε>0 and calculate the f(x) limit when x approaches ε.
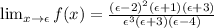
Notice that the numerator is positive for any small value of ε>0. On the other hand, regarding the denominator (ε^3)>0, (ε+3)>0, (ε-4)<0. There is a negative value in the denominator!
Therefore, the function approaches -infinite as x->0 from the right
