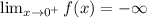Question

Consider the function…at the vertical asymptote, x = 0, predict the behavior of the function approaching the asymptote from the right.

Answer 1

The function is

`f(x)=((x-2)^2(x+1)(x+3))/(x^3(x+3)(x-4))`

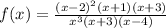
Notice that if we try to evaluate the function at x=0, we would get,

`\lim _(x\to0)f(x)=(12)/(0)`

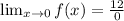
This means that the function f(x) goes to infinity as x approaches zero.

Consider a very small value ε>0 and calculate the f(x) limit when x approaches ε.

`\lim _(x\to\epsilon)f(x)=((\epsilon-2)^2(\epsilon+1)(\epsilon+3))/(\epsilon^3(\epsilon+3)(\epsilon-4))`

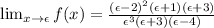
Notice that the numerator is positive for any small value of ε>0. On the other hand, regarding the denominator (ε^3)>0, (ε+3)>0, (ε-4)<0. There is a negative value in the denominator!

Therefore, the function approaches -infinite as x->0 from the right

`\lim _(x\to0^+)f(x)=-\infty`