Assume that,
The two angles of one triangle are congruent to two angles of a second triangle.
To prove: The third angles of the triangles are congruent.
Since, two angles of one triangle are congruent to two angles of a second triangle.
Therefore,
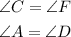
Adding these two we get,
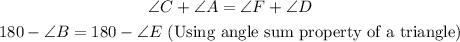
Cancelling 180 on both sides, we get
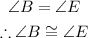
Hence, if two angles of one triangle are congruent to two angles of a second triangle, the the third angles of the triangles are congruent.