Question

A standard roulette wheel contains the numbers 1-36, and two spaces marked "0" and "00." Halfof the numbers are labeled black, and half of the numbers are labeled red. The numbers "0" and“00” are labeled greenfield . Half of the red and black slots have even numbers, the other half oddnumbers. When the wheel is spun, a ball rolls along the outer edge of the wheel until it falls intoone of the numbered slots. What is the probability that the ball lands on an even number or ablack number?

Answer 1

let E be the total outcomes

The standard number wheel contains 36 numbers and two spaces marked

The total sample space will be 38

n(E)=38

let B be the number of blacck, R be the nunber of red and G be the number of green

Number of Black, n(B) = 18

Number of Red, n(R) =18

Number of green , n(G)=2

Let the number of Black and red be

the Probability of an event is given n(RnB)=9

`\frac{\text{reuire outcome }}{total\text{ outcome}}`

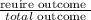
Probability that the balls lands on an even number or a black number is given by

`\begin{gathered} P(R)\text{ +P(B) -P(R n B)} \\ \end{gathered}`
`\begin{gathered} P(R)=(n(R))/(n(E))=(18)/(38) \\ P(B)=(n(B))/(n(E))=(18)/(38) \\ P(\text{RnB)}=\frac{n(\text{RnB)}}{n(E)}=(9)/(38) \end{gathered}`

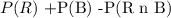
Therefore we have

`\begin{gathered} (18)/(38)+(18)/(38)-(9)/(38) \\ (18+18-9)/(38)=(27)/(38) \end{gathered}`

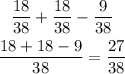
Therefore the probability that the balls lands on an even number or a black number is 27/38 or 0.71