Question

PO is the perpendicular bisector of MON. MP= 2x+5, angle measure OPN= 5x+101. find the value of x2. find MN

Answer 1

Given:

PO is the perpendicular bisector of triangle MON.

`\begin{gathered} MP=2x+5 \\ \angle OPN=5x+10 \end{gathered}`

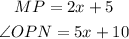
1. To find the value of x:

Since,

`OP\perp MN`

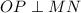
Therefore, the angle measure of OPN is 90 degrees.

So that,

`\begin{gathered} \angle OPN=90^(\circ) \\ 5x+10=90 \\ 5x=80 \\ x=16 \end{gathered}`

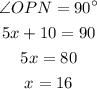
Hence the value of x is 16.

2. To find MN:

Since PO is the perpendicular bisector to the side MN.

So, MP=PN

Therefore,

`\begin{gathered} MN=MP+PN \\ =MP+MP \\ =2MP \\ =2(2x+5) \\ =4x+10 \\ =4(16)+10\text{ \lbrack{}Substituting x = 16\rbrack} \\ =64+10 \\ MN=74 \end{gathered}`

Hence, the length of MN is 74.