Step-by-step explanation
To solve this problem, we will use the formula for compound interest:
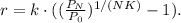
Where:
• Pₙ = principal amount after N years,
,
• P₀ = initial principal amount,
,
• r = interest ratio in decimals,
,
• k = compound periods per year.
From the statement, we know that:
• N = 3.4 years,
• P₀ = $56,000,
• Pₙ = P₀ + interest = $56,000 + $1,400 = $57,400,
,
• r = ?,
,
• k = 4 (the interest is compounded quarterly.
Replacing these values in the formula above, we get:
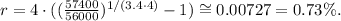
Answer
The annual interest must be 0.73%.