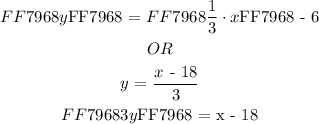We are to determine the equation of line by interpreting tabulated results between an independent variable ( x ) and a dependent variable ( y ).
A function is usually expressed as follows:
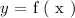
The above notation gives us the output ( y ) which is a function of input variable ( x ). This means that whatever relationship these two variables have the value of output ( y ) is related to the imput variable ( x ).
We are given a table/list of values of output ( y ) corresponding to each value of input variable ( x ) as follows:
Input ( x ) Output ( y )
3 -5
6 -4
9 -3
There are a series of steps that we must take to arrive at the equation that relates two variables.
Step 1: Determine the type of relationship between two variables by intuition
The first step in the process is the hardest of all. We have to critically analyze each input value ( x ) and its corresponding output value ( y ) with successive pair of values.
There are many types of relationships possible ( polynomial order, exponential, logarithmic, trigonometric, radical, etc .. ).
We can conjure up a way by comparing outputs of successive values to determine the type of relationship possible.
So looking at the first value:
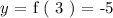
The successive value:
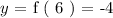
The next successive value:
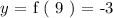
Here if scrutinize between each successive value of input variable ( x ) we see that there is a "3 unit step-up" in each pair of values i.e ( 3 -> 6 -> 9 ).
Next we compare each output values ( y ) for successive pairs. We see that with every step increase of 3 units in ( x ) value there is an increase of ( 1 ) unit in output value i.e ( -5 -> -4 -> -3 ).
Conclusion: Combing the result of above analysis we see that with each 3 step increase in input value ( x ) there is an increase in output value ( y ) by 1 unit.
This gives us the idea that the two variables are linearly related to one another.
Therefore, the type of relationship is:
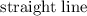
Step 2: Recall the equation for the type of relationship between two vairbales x and y
Once we have determined the type of relationship between two variables. We will have to resort to our equation bank and pluck out the corresponding equation that expresses a LINEAR relationship i.e equation of a straight line.
The slope-intercept form of a straight line is:
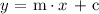
Step 3: Determine the complete equation of function by defining the arbitrary constants.
The above equation is valid for all straight lines that express a linear relationship. However, we seek to find a unique straight line for the given set of points.
Every unique straight line equation would have either of the constants different. The constants defined in a striaght line equation are:
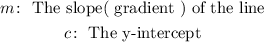
To determine these constants we will use the given pairs of coordinates of input and output variables, x and y respectively.
To determine the slope (m) of an equation:
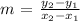
The above expression relates the change in output value ( y ) with respect to change in input variable ( x ).
To determine the constant ( m ) we will use the conclusion from Step 1:
"3 step increase in input of ( x ) value there is an increase in output value ( y ) by 1 unit."
Therefore,
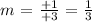
To determine the value of y-intercept ( c ). We will plug in the value of ( m ) into the general equation of a straight line written in step 2:
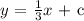
Now, we will use any pair of input and output value.
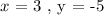
Substitute the pair of values into the derived equation expressed above and solve for constant ( c ):
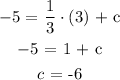
Note: The above step implies that following equation must satisfy each and every data pair of point given to us ( table ). Or each and every value must lie on the line. For that each value must satisfy the equation of line.
Step 4: Write the complete equation of the relationship
Once we have evaluated the values of equation defining constants ( m and c ). We can simply plug in the values into the general equation relationship ( Linear - slope intercept form ) as follows:
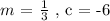
Therefore, the equation for the set of values given to us is: