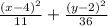Given
Major axis of length = 12
Foci at ( 9 ,1 ) and ( -1, 1 )
Find
Equation of an ellipse
Step-by-step explanation
As we know , major axis = 2a = 12
thus a = 6
the midpoint between the foci is the center , so

the distance between the foci is equal to 2c
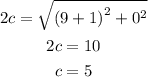
now,
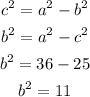
so , the equation of an ellipse is
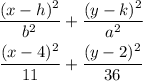
Final Answer
The equation of an ellipse