I would start by stating the Fundamental Theorem of Calculus which states that;
If a function f is continuous on a closed interval [a,b] and F is an antiderivative of f on the interval [a,b], then
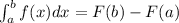
Let
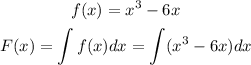
Recall that;
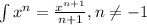
That implies that,

Applying the Fundamental Theorem of Calculus, where a=0, b=3
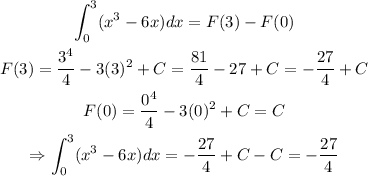
So the answer is -27/4