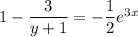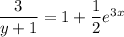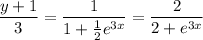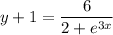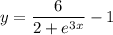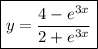Question

Problem 4: Solve the initial value problem


`y' = (y + 1)(y - 2)`

`y(0) = 1`
​

Answer 1

Separate the variables:

`y' = (dy)/(dx) = (y+1)(y-2) \implies \frac1{(y+1)(y-2)} \, dy = dx`

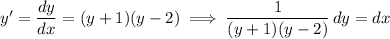
Separate the left side into partial fractions. We want coefficients a and b such that

`\frac1{(y+1)(y-2)} = \frac a{y+1} + \frac b{y-2}`

`\implies \frac1{(y+1)(y-2)} = (a(y-2)+b(y+1))/((y+1)(y-2))`

`\implies 1 = a(y-2)+b(y+1)`

`\implies 1 = (a+b)y - 2a+b`

`\implies \begin{cases}a+b=0\\-2a+b=1\end{cases} \implies a = -\frac13 \text{ and } b = \frac13`

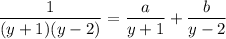
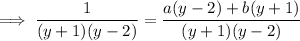
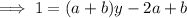
So we have

`\frac13 \left(\frac1{y-2} - \frac1{y+1}\right) \, dy = dx`

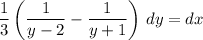
Integrating both sides yields

`\displaystyle \int \frac13 \left(\frac1{y-2} - \frac1{y+1}\right) \, dy = \int dx`

`\frac13 \left(\ln|y-2| - \ln|y+1|\right) = x + C`

`\frac13 \ln\left|(y-2)/(y+1)\right| = x + C`

`\ln\left|(y-2)/(y+1)\right| = 3x + C`

`(y-2)/(y+1) = e^(3x + C)`

`(y-2)/(y+1) = Ce^(3x)`

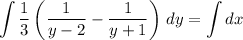
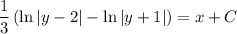
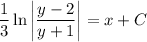
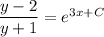
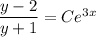
With the initial condition y(0) = 1, we find

`(1-2)/(1+1) = Ce^(0) \implies C = -\frac12`

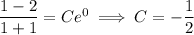
so that the particular solution is

`\boxed{(y-2)/(y+1) = -\frac12 e^(3x)}`

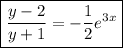
It's not too hard to solve explicitly for y; notice that

`(y-2)/(y+1) = ((y+1)-3)/(y+1) = 1-\frac3{y+1}`

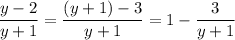
Then

`1 - \frac3{y+1} = -\frac12 e^(3x)`

`\frac3{y+1} = 1 + \frac12 e^(3x)`

`\frac{y+1}3 = \frac1{1+\frac12 e^(3x)} = \frac2{2+e^(3x)}`

`y+1 = \frac6{2+e^(3x)}`

`y = \frac6{2+e^(3x)} - 1`

`\boxed{y = (4-e^(3x))/(2+e^(3x))}`