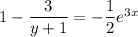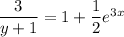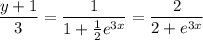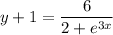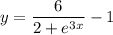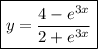Separate the variables:
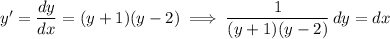
Separate the left side into partial fractions. We want coefficients a and b such that
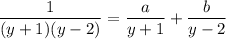
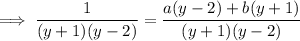
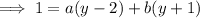
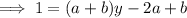

So we have
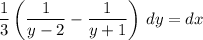
Integrating both sides yields
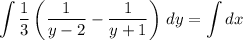
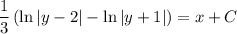
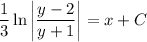
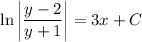
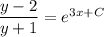
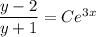
With the initial condition y(0) = 1, we find
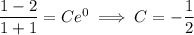
so that the particular solution is
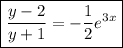
It's not too hard to solve explicitly for y; notice that
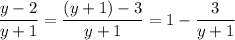
Then