Answer:
• Equations
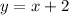
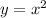
• Solutions (2, 4) and (–1, 1)
Step-by-step explanation
System of equations
• Linear equation
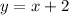
• Quadratic equation
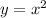
We have to set both equations to 0 and equalize them:
• 1. Setting them to 0:
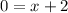
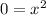
• 2. Equalizing them:
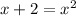
To solve the system using the General Quadratic Formula, we have to set the equation in the form ax² + bx+ c = 0:
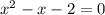
Thus, in this case a = 1, b = -1 and c = -2. Using the formula:

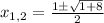
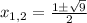
Finding both solutions:
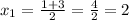
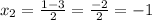
Finally, replacing these values in the linear equation to find y:
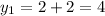
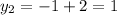
Therefore, the solutions are (2, 4) and (–1, 1).