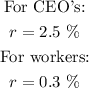The exponential growth formula is given by
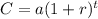
where C is the average compensation, a is the initial amount and t is the time (in years).
For the CEO's case, we have that
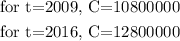
Then, we can find a and r with these values. By substituting the first values, we have
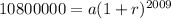
By substituting the second values, we get
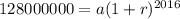
By isolating a in both case, we have that
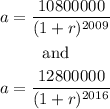
Then, we can state the following equation:
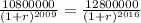
or equivalently,
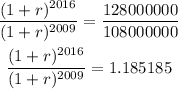
By applying natural logarithm in bot sides, we have
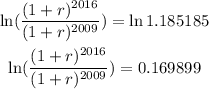
By the properties of logarithms:
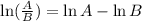
we obtain
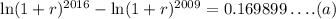
By the property of logaritm:
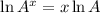
The last result is equivalent to
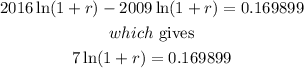
then, by moving the number 7 to the right hand side, this yields,
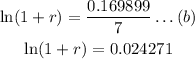
Now, by applying the exponential function in both sides, we have

then, r is given by
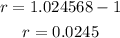
Now, by converting this result into percent form. The answer for the CEO's case is
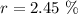
Now, for the workers case, we can do the same procedure and get an equation similar to equation (a). That is,
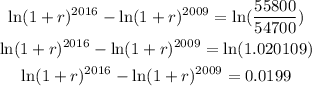
and find somthing similar to equation (b)
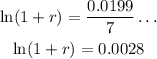
and finally,
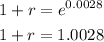
then, r will be
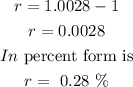
In summary,by rounding the answers to the nearest tenth percent, the answers are