Question

Options for the first box:(2x-1)(x+9), (2x+1)(x-9), x+7, 3x(x-9) Options for second box: x-7, 3x(x+7), 3x(2x+1), x+7 Options for the third box: -7, 9, -0.5, 0.5, 0

Answer 1

To determine the value of the quotient of a polynomial function:

`(3x^2-27x)/(2x^2+13x-7)\text{ x }(4x^2-1)/(3x)`

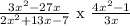
The quotient consists of the numerator which represents the first box

while the denominator represents the second box

`\begin{gathered} (3x^2-27x)/(2x^2+13x-7)\text{ x}(4x^2-1)/(3x) \\ (3x(x-9))/(2x^2+14x-x-7)\text{ x}((2x)^2-1)/(3x) \\ \frac{3x(x-9)}{2x(x_{}+7)-1(x+7)}\text{ x }((2x-1)(2x+1))/(3x) \\ (3x(x-9)(2x-1)(2x+1))/((2x-1)(x+7)3x) \end{gathered}`
`((x-9)(2x+1))/((x+7))`

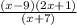
Therefore the simplest form of the quotient has a numerator of (x-9)(2x+1) and a denominator of (x+7)

The expression does exist when x = 0