Question

Determine without graphing wether the given quadratic function has a maximum value or a minimum value and find the value 6x^2-12x

Answer 1

You have the following quadratic function:

`6x^2-12x`

the previous function is a parabolla with a positive leading coefficient equal to 6 (leadding coefficient is the coefficient of the quadratic term). It means that the parabola opens up and then the parabolla has a minimum point.

The x-coordinate of the minimum point is just the x-coordinate of the vertex, which is given by:

`x=-(b)/(2a)`

a and b are coefficients of the quadratic function. In this case a=6 and b=-12.

Replace the previous parameters into the expression for x and simplify:

`x=-(-12)/(2(6))=(12)/(12)=1`

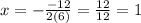
Now, the y-coordinate of the vertex (minimum point in this case) is:

`y=6(1)^2-12(1)=6-12=-6`

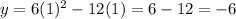
Then, the minimum of the function is at the point (1 , -6)