Question

The coordinates of two vertices of square ABCD are A(2, 1) and B(4,4). Determine the slope of side BC.PleasE HELP

Answer 1

`Slope_(sideBC)=-(2)/(3)`

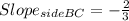
Step-by-step explanation

Step 1

if ABCD is a square then, the segment AB must be perpendicular to segment BC

it means,( if two lines are perpendicular, the product of the slopes is -1)

`\text{slope}1\cdot\text{slope}2=-1\text{ equation (1)}`

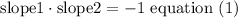
Step 2

find the slope of segment AB

Let P1(2,1) P2(4,4)

`\begin{gathered} \text{slope}=(y_2-y_1)/(x_2-x_1) \\ \text{replacing} \\ \text{slope}=(4-1)/(4-2) \\ \text{slope1}=(3)/(2) \end{gathered}`

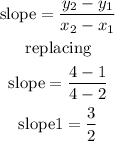
Step 3

replace in equation (1) to find the slope of side BC

`\begin{gathered} (3)/(2)\cdot\text{slope}2=-1 \\ \text{slope}_(2=)-1\cdot(2)/(3) \\ \text{slope}2=-(2)/(3) \end{gathered}`

slope2= slope of side BC

I hope this helps you