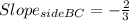
Step-by-step explanation
Step 1
if ABCD is a square then, the segment AB must be perpendicular to segment BC
it means,( if two lines are perpendicular, the product of the slopes is -1)
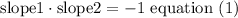
Step 2
find the slope of segment AB
Let P1(2,1) P2(4,4)
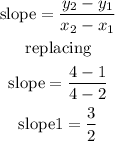
Step 3
replace in equation (1) to find the slope of side BC
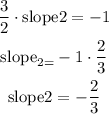
slope2= slope of side BC
I hope this helps you