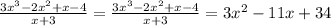Answer:
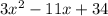
Explanation:
Given the division below:
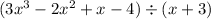
First, set the denominator equal to 0 and solve for x.
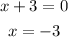
Next, set the synthetic division table as shown below:
• Bring down the leading coefficient, 3.
,
• Then multiply 3 by -3, write the result in the next column and add.
Repeat the process until you get the sum of the last column.
Therefore:
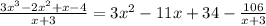
Following the instruction in the question, we ignore the remainder and write: