Question

In a rescue, the 65.0-kg police officer is suspended
by two cables, as shown in (Figure 1).

Answer 1

how high is the police officer, if he's not high,

Step-by-step explanation:

CUT HIM DOWN!

lol

Answer 2

The tension in the right cable is 525.7 N

How to determine this?

The person is in equilibrium, indicating that the net horizontal force
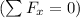`(\(\sum F_x = 0\))` and the net vertical force
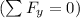`(\(\sum F_y = 0\))` acting on them are both zero.

For the horizontal equilibrium:

`\[ T_(R) \cdot \cos 48^\circ - T_(L) \cdot \cos 35^\circ = 0 \]`

`\[ T_(R) = \left( (\cos 35^\circ)/(\cos 48^\circ) \right) T_(L) \]`

For the vertical equilibrium:

`\[ T_(R) \cdot \sin 48^\circ + T_(L) \cdot \sin 35^\circ - W = 0 \]`

`\[ \left( (\cos 35^\circ)/(\cos 48^\circ) \cdot T_(L) \right) \cdot \sin 48^\circ + T_(L) \cdot \sin 35^\circ - mg = 0 \]`

`\[ T_(L) \cdot (\cos 35^\circ \cdot \tan 48^\circ + \sin 35^\circ) = mg \]`

`\[ T_(L) = (mg)/(\cos 35^\circ \cdot \tan 48^\circ + \sin 35^\circ) \]`

Given:
`\( m = 65 \, \text{kg} \), \( g = 9.8 \, \text{m/s}^2 \)`

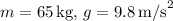
Substituting the values:

`\[ T_(L) = \frac{(65 \, \text{kg}) * (9.8 \, \text{m/s}^2)}{\cos 35^\circ \cdot \tan 48^\circ + \sin 35^\circ} \]`

`\[ T_(L) = 429.4 \, \text{N} \]`

Subsequently, for
`\( T_(R) \)`:

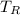`\[ T_(R) = \left( (\cos 35^\circ)/(\cos 48^\circ) \right) * (429.4 \, \text{N}) \]`

`\[ T_(R) = 525.7 \, \text{N} \]`

Therefore. the tension in the right cable is 525.7 N,

Complete question:

Find the tension in the right cable.

Express your answer in newtons