Answer:
Step-by-step explanation:
At x = 3, we have y = 0
This means x = 3 is a root.
Let the cubic function be:
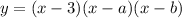
When x = 1, y = -2, so
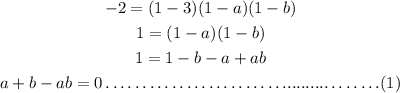
SImilarly, when x = 2, y = -1
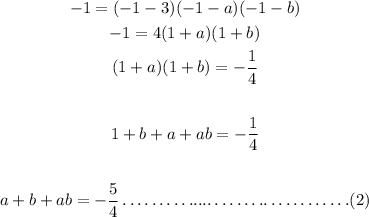
Adding (1) and (2)
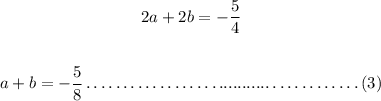
Subtracting (1) from (2)
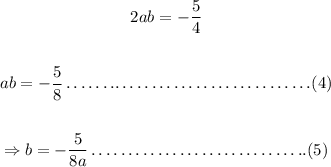
Using (5) in (3)
![\begin{gathered} a-(5)/(8a)=-(5)/(8) \\ \\ 8a^2-5=-5a \\ 8a^2+5a-5=0 \\ a=(-5)/(16)-\sqrt[]{(185)/(16)} \\ \\ OR \\ (-5)/(16)+\sqrt[]{(185)/(16)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/krmz8o4cgwebz4i64iu1kizzjl2zzb2vwf.png)
Therefore, for b, we have:
![\begin{gathered} b=(1)/(16)(√(185)-5) \\ OR \\ b=(1)/(16)(-5-\sqrt[]{185}) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a4yr3f0f7zqxrcukzl1x3k2vuksczencef.png)
Replacing a and b by these values obtained, we have the required cubic function