Question

Decide whether the following lines are parallel, perpendicular, or neither. y = - 13x + 3 5 1-7X-2 ha horren

Answer 1

Neither

Step-by-step explanation:

Given the equations;

`\begin{gathered} y=-13x+3 \\ y=(5)/(2)x-2 \end{gathered}`

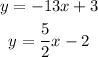
We want to determine if they are parallel, perpendicular or neither.

Recall that;

For them to be parallel, they must have the same slope.

`m_1=m_2`

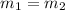
For them to be perpendicular their slope must be negative reciprocal of one another.

`m_1m_2=-1`

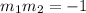
For the given equations; with slopes;

`\begin{gathered} m_1=-13 \\ m_2=(5)/(2) \end{gathered}`

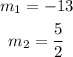
They are not parallel;

`\begin{gathered} m_1\\e m_2 \\ -13\\e(5)/(2) \end{gathered}`

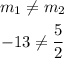
Also, they are not perpendicular;

`\begin{gathered} m_1m_2\\e-1 \\ -13((5)/(2))\\e-1 \end{gathered}`

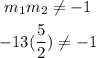
Therefore, the two equations are neither parallel nor perpendicular.