Answer:
Neither
Step-by-step explanation:
Given the equations;
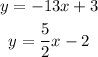
We want to determine if they are parallel, perpendicular or neither.
Recall that;
For them to be parallel, they must have the same slope.
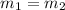
For them to be perpendicular their slope must be negative reciprocal of one another.
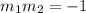
For the given equations; with slopes;
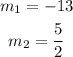
They are not parallel;

Also, they are not perpendicular;
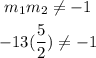
Therefore, the two equations are neither parallel nor perpendicular.