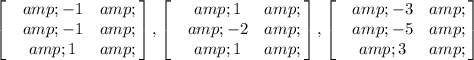Question

Please help with this question. Im struggling a little bit

Answer 1

Given:

`A=\begin{bmatrix}{4} & {6} & {10} \\ {3} & {10} & {13} \\ {-2} & {-6} & {-8}\end{bmatrix}`

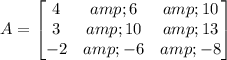
First we need to find the eigenvalues of A. Recall that they are the solutions of the equation det(λI - A) = 0:

`det\lparenλ\begin{bmatrix}{1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {0} & {1}\end{bmatrix}-\begin{bmatrix}{4} & {6} & {10} \\ {3} & {10} & {13} \\ {-2} & {-6} & {-8}\end{bmatrix})=0`

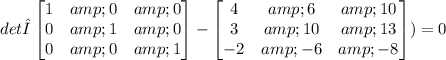
which becomes

`det\lparen\begin{bmatrix}{λ}-4 & {-6} & {-10} \\ {-3} & {λ-10} & {-13} \\ {2} & {6} & {λ+8}\end{bmatrix})=0`

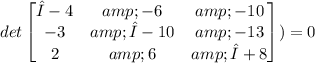
Calculate this determinant:

`\begin{gathered} (λ-4)(λ-10)(λ+8)+(-3)(6)(-10)+(2)(-6)(-13) \\ -(-10)(λ-10)(2)-(-6)(-3)(λ+8)-(-13)(6)(λ-4)=0 \end{gathered}`

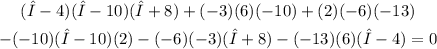
Simplify:

`λ^3-6λ^2+8λ=0`

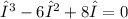
Then, factor:

`λ(λ-2)(λ-4)=0`

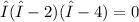
Separate the solutions:

`\begin{gathered} λ=0\text{ or} \\ λ-2=0 \\ λ-2+2=0+2 \\ λ=2\text{ or} \\ λ-4=0 \\ λ-4+4=0+4 \\ λ=4 \end{gathered}`

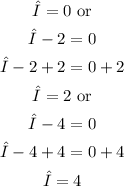
Now that we have found the eigenvalues for A , we can compute the eigenvectors:

For λ = 0

`\begin{bmatrix}{-1} & & \\ {-1} & & \\ {1} & & \end{bmatrix}`

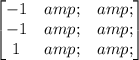
For λ = 2

`\begin{bmatrix}{} & {1} & {} \\ {} & {-2} & {} \\ {} & {1} & {}\end{bmatrix}`

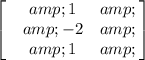
For λ = 4

`\begin{bmatrix}{} & {-3} & {} \\ {} & {-5} & {} \\ {} & {3} & {}\end{bmatrix}`

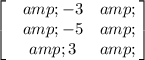
Answer:

The eigenvalues are:

`\begin{gathered} λ=0 \\ λ=2 \\ λ=4 \end{gathered}`

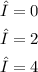
And the eigenvectors are:

`\begin{bmatrix}{} & -{1} & {} \\ {} & {-1} & {} \\ {} & {1} & {}\end{bmatrix},\begin{bmatrix}{} & {1} & {} \\ {} & {-2} & {} \\ {} & {1} & {}\end{bmatrix},\begin{bmatrix}{} & {-3} & {} \\ {} & {-5} & {} \\ {} & {3} & {}\end{bmatrix}`