Question

Determine the value of the angle. Round to the nearest tenth. (G.8c)(1 point) 25m 16m

Answer 1

Step-by-step explanation:

For any right triangle

the relationship between the hypotenuse and the adjacent side of an angle theta is the cosine of the angle:

`\cos \theta=(b)/(a)`

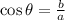
In this problem we have b = 16m and a = 25m. Therefore the cosine of x is:

`\cos x=(16m)/(25m)=0.64`

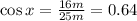
Using the inverse of the cosine - "the arc whose cosine is x" - we find x:

`\begin{gathered} x=\arccos 0.64 \\ x\approx50.21º\approx0.88rad \end{gathered}`

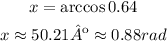
Answer:

The value of the angle is x = 50.21º or x = 0.88 radians