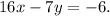Question

write an equation of the line through (-3, -6) having slope 16/7. give the answer in standard form.The equation of the line is ? x- ? y= ?

Answer 1

Recall that the equation of a line in standard form is as follows:

`Ax+By=C,`

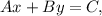
where A, B, and C are integers and A>0.

Now, to answer this question we will use the following slope-point formula for the equation of a line:

`y-y_1=m(x-x_1)\text{.}`

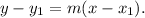
Therefore the equation of the line that passes through (-3,-6) and has a slope of 16/7 is:

`y-(-6)=(16)/(7)(x-(-3))\text{.}`

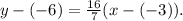
Simplifying the above result we get:

`y+6=(16)/(7)(x+3)\text{.}`

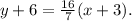
Multiplying the above equation by 7 we get:

`\begin{gathered} 7*(y+6)=7*(16)/(7)(x+3), \\ 7(y+6)=16(x+3)\text{.} \end{gathered}`

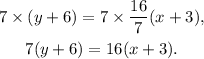
Applying the distributive property we get:

`\begin{gathered} 7\cdot y+7\cdot6=16\cdot x+16\cdot3, \\ 7y+42=16x+48. \end{gathered}`

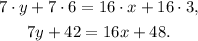
Subtracting 7y from the above equation we get:

`\begin{gathered} 7y+42-7y=16x+48-7y, \\ 42=16x+48-7y\text{.} \end{gathered}`

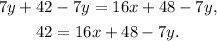
Subtracting 48 from the above equation we get:

`\begin{gathered} 42-48=16x+48-7y-48, \\ -6=16x-7y\text{.} \end{gathered}`

Answer:

`16x-7y=-6.`