We have to find the marginal cost of the function:
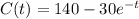
for the value t=6. We remember that the marginal cost is defined as the derivative of the function of total cost. So, for finding the value of marginal cost, we will find its function:
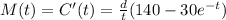
Then, using the properties of differentiation,
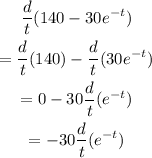
And then, for finding the last derivative, we use the chain rule:
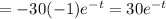
This means that our marginal cost function is:
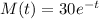
Finding the value when t=6
We just have to find the value M(6), by replacing t by 6, as shown:
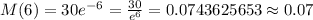
This means that the marginal cost when t=6 is 0.07 million dollars per year.