When two variables are inversely proportional we can represent them in the following manner:

Where "a" would be the constant of proportionality. In the case of our problem the y is inversely proportional to the square of "x", this means that the correct expression is:
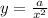
We need to find the value of "a", to do that we will apply the ordered pair which was given to us (17,8).

Therefore the expression to this problem is:
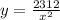
We want to find the value of "y" when "x" is equal to 14, therefore:
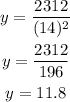
The value of "y" is 11.8