Let A represent point (3,8) and B represent point (-5,5)
To find the distance between Points A and B you have to calculate the difference between the x-coordinates and the difference between the y-coordinates of both points:
In the diagram I uploaded I marked the distance over the x and y axis with blue lines and determined a triangle. The distance over the x-axis represents the base of the triangle "a"
Base:

The base of the triangle is a=8
The distance over the y-axis is the height of the triangle "b", you have to calculate as the difference between both y-coordinates:
Height:
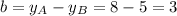
The height of the triangle is b=3
Finally the distance between both points (black line) is the hypothenuse of the triangle. To calculate this distance you have to apply Pythagoras theorem, this theorem states that the square of the hypothenuse is equal to the sum of the squares of the base and height of the triangle:
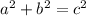
Replace it using the calculated values a=8 and b=3