Question

The terms of a sequence are given. Use these terms to answer the following questions. 2, 8, 14, 20, 26 Write a RECURSIVE rule & an EXPLICIT rule to represent the arithmetic sequence. Make sure to explain how you got your answer.

Answer 1

The given sequence is

`2,8,14,20,26`

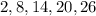
The standard Explicit formula for an arithmetic sequence is given by

`a_n=a_1+(n-1)d`

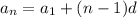
Where aₙ is the nth term, a₁ is the first term and d is the common difference

The common difference is basically the difference between any two consecutive terms

d = 26 - 20 = 6

d = 20 - 14 = 6

d = 14 - 8 = 6

d = 8 - 2 = 6

So the common difference is 6

The first term in the sequence is 2

So the Explicit formula for an arithmetic sequence becomes

`a_n=2+(n-1)\cdot6`

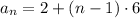
Now let us find the Recursive rule of this arithmetic sequence

`a_n=a_(n-1)+d`

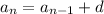
Where aₙ is the nth term, aₙ₋₁ is the previous term of the nth term, and d is the common difference

We already know the common difference is 6

So the Recursive rule for an arithmetic sequence becomes

`a_n=a_(n-1)+6`

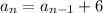
Therefore, the RECURSIVE rule & EXPLICIT rules are

`\begin{gathered} Recursive\: Rule\colon\: \: a_n=a_(n-1)+6 \\ Explicit\: Rule\colon\: \: a_n=2_{}+(n-1)\cdot6 \end{gathered}`

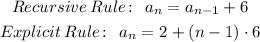
Let us simplify the above explicit rule

`\begin{gathered} a_n=2+(n-1)\cdot6 \\ a_n=2+6n-6 \\ a_n=6n+2-6 \\ a_n=6n-4 \end{gathered}`

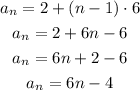
Therefore, the above explicit rule is also valid.